Gradient Accumulation: Increase Batch Size Without Explicitly Increasing Batch Size
An underrated technique to train neural networks in memory constrained settings.
Under memory constraints, it is always recommended to train the neural network with a small batch size.
Despite that, there’s a technique called gradient accumulation, which lets us (logically) increase batch size without explicitly increasing the batch size.
Confused?
Let’s understand this today.
But before that, we must understand…
Why do neural networks typically explode during training?
The primary memory overhead in a neural network comes from backpropagation.
This is because, during backpropagation, we must store the layer activations in memory. After all, they are used to compute the gradients.
The bigger the network, the more activations a network must store in memory.
Also, under memory constraints, having a large batch size will result in:
storing many activations
using those many activations to compute the gradients
This may lead to more resource consumption than available — resulting in training failure.
But by reducing the batch size, we can limit the memory usage and train the network.
What is Gradient Accumulation and how does it help in increasing batch size in memory constraints?
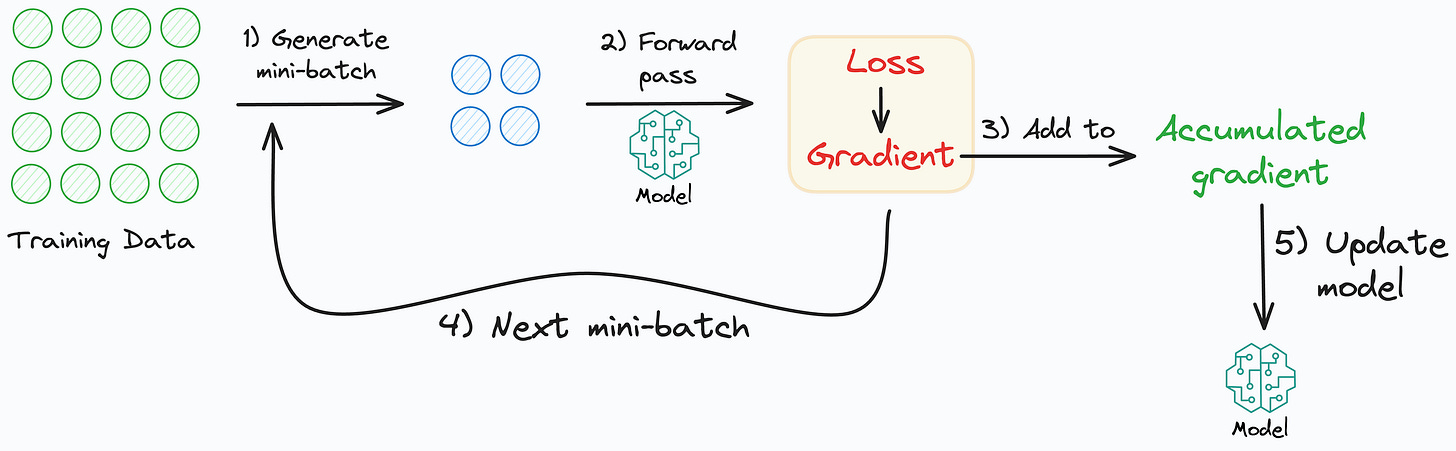
Consider we are training a neural network on mini-batches.
We train the network as follows:
On every mini-batch:
Run the forward pass while storing the activations.
During backward pass:
Compute the loss
Compute the gradients
Update the weights
Gradient accumulation modifies the last step of the backward pass, i.e., weight updates.
More specifically, instead of updating the weights on every mini-batch, we can do this:
Run the forward pass on a mini-batch.
Compute the gradient values for weights in the network.
Don’t update the weights yet.
Run the forward pass on the next mini-batch.
Compute the gradient values for weights and add them to the gradients obtained in step 2.
Repeat steps 3-5 for a few more mini-batches.
Update the weights only after processing a few mini-batches.
This technique works because accumulating the gradients across multiple mini-batches results in the same sum of gradients as if we were processing them together.
Thus, logically speaking, using gradient accumulation, we can mimic a larger batch size without having to explicitly increase the batch size.
For instance, say we want to use a batch size of 64. However, current memory can only support a batch size of 16.
No worries!
We can use a batch size of size 16.
We can accumulate the gradients from every mini-batch.
We can update the weights only once every 8 mini-batches.
Thus, effectively, we used a batch size of 16*8 (=128) instead of what we originally intended — 64.
Cool, right?
Implementation
Let’s look at how we can implement this.
In PyTorch, a typical training loop is implemented as follows:
We clear the gradients
Run the forward pass
Compute the loss
Compute the gradients
Update the weights
However, as discussed earlier, if needed, we can only update the weights after a few iterations.
Thus, we must continue to accumulate the gradients, which is precisely what loss.backward() does.
Also, as optimizer.zero_grad() clears the gradients, we must only execute it after updating the weights.
This idea is implemented below:
First, we define
acc_steps— the number of mini-batches after which we want to update the weights.Next, we run the forward pass.
Moving on, we compute the loss and the gradients.
As discussed earlier, we will not update the weights yet and instead let the gradients accumulate for a few more mini-batches.
We only update the weights when the if condition is true.
After updating, we clear the accumulated gradients.
Done!
This way, we can optimize neural network training in memory-constrained settings.
Before we end, it is essential to note that gradient accumulation is NOT a remedy to increase run-time in memory-constrained situations.
In fact, we can also verify this from my experiment:
Both possess nearly the same run-time.
Instead, its objective is to reduce overall memory usage.
Of course, it’s true that we are updating the weights only after a few iterations. So, it will be a bit faster than updating on every iteration.
Yet, we are still processing and computing gradients on small mini-batches, which is the core operation here.
Nonetheless, the good thing is that even if you are not under memory constraints, you can still use gradient accumulation.
Specify your typical batch size.
Run forward pass.
Compute loss and gradients.
Update only after a few iterations.
Isn’t that a cool technique?
You can download the notebook here: Jupyter Notebook.
👉 Over to you: What are some other ways to train neural networks in memory-constrained situations?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed last month:
Why Bagging is So Ridiculously Effective At Variance Reduction?
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit
Model Compression: A Critical Step Towards Efficient Machine Learning.
Generalized Linear Models (GLMs): The Supercharged Linear Regression.
Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.
Formulating and Implementing the t-SNE Algorithm From Scratch.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!