Maximum Likelihood Estimation vs. Expectation Maximization — What’s the Difference?

A popular interview question.

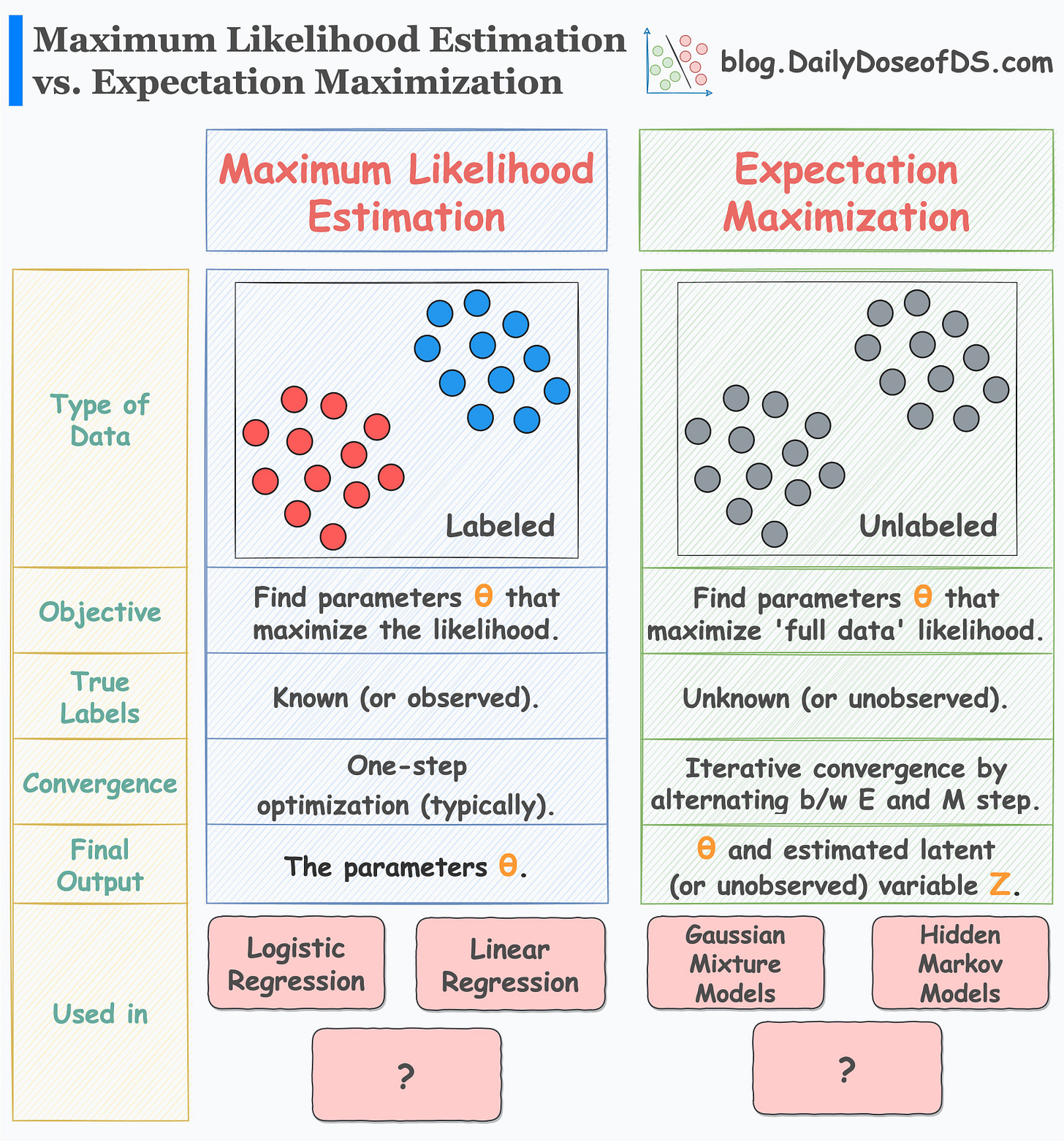
Maximum likelihood estimation (MLE) is a popular technique to estimate the parameters of statistical models.

Given some labeled data, find the model parameters.

The process is pretty simple and straightforward.

In MLE, we:

• Start by assuming the data generation process.

Assume a data generation process

• Next, we define the likelihood of observing the data, given some parameter values for the model.

Define the likelihood function

• Lastly, we maximize the above function to get the parameters.

As a result, we get an estimate for the parameters that would have most likely generated the given data.

But what to do if we don’t have true labels but you still wish to estimate the parameters?

Unlabeled data

MLE, as you may have guessed, will not be useful.

The true label, being unobserved, makes it impossible to define a likelihood function.

In such cases, advanced techniques like Expectation-Maximization are quite helpful.

It’s an iterative optimization technique to estimate the parameters of statistical models.

It is particularly useful when we have an unobserved (or hidden) label.

One example situation could be as follows:

Data from multiple distributions

We assume that the data was generated from multiple distributions (a mixture). However, the observed data does not hold that information.

In other words, we don’t know whether a specific row was generated from distribution 1 or distribution 2.

The core idea behind EM is as follows:

• Make a fair guess about the initial parameters.

• Expectation (E) step: Compute the posterior probabilities of the unobserved variable using current parameters.

z, at times, is also called a latent variable. “Latent” means unobserved. We know it exists, but we don’t know what it is.

• Define the “expected likelihood” function using the above posterior probabilities.

• Maximization (M) step: Update the current parameters by maximizing the “expected likelihood.”

• Use the updated parameters to recompute the posterior probabilities, i.e., Back to E-step.

• Repeat until convergence.

A good thing about EM is that it always converges. Yet, at times, it might converge to a local extrema.

The visual below neatly summarizes the differences between MLE and EM:

MLE vs. EM is a popular question asked in many data science interviews.

For those who are interested in:

• practically learning about Expectation Maximization

• and programming it from scratch...

….then we covered it in detail in a recent article as well: Gaussian Mixture Models: The Flexible Twin of KMeans.

👉 Over to you: What are some other differences between MLE and EM?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

Thanks for reading!

---

Latest full articles

If you’re not a full subscriber, here’s what you missed last month:

• Formulating and Implementing the t-SNE Algorithm From Scratch.

• Generalized Linear Models (GLMs): The Supercharged Linear Regression.

• Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.

• Bayesian Optimization for Hyperparameter Tuning.

• Formulating the PCA Algorithm From Scratch.

• Where Did The Assumptions of Linear Regression Originate From?

To receive all full articles and support the Daily Dose of Data Science, consider subscribing:

---

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!