The Most Common Misconception About Continuous Probability Distributions

The difference between probability density function and probability.

Let me ask you a question today.

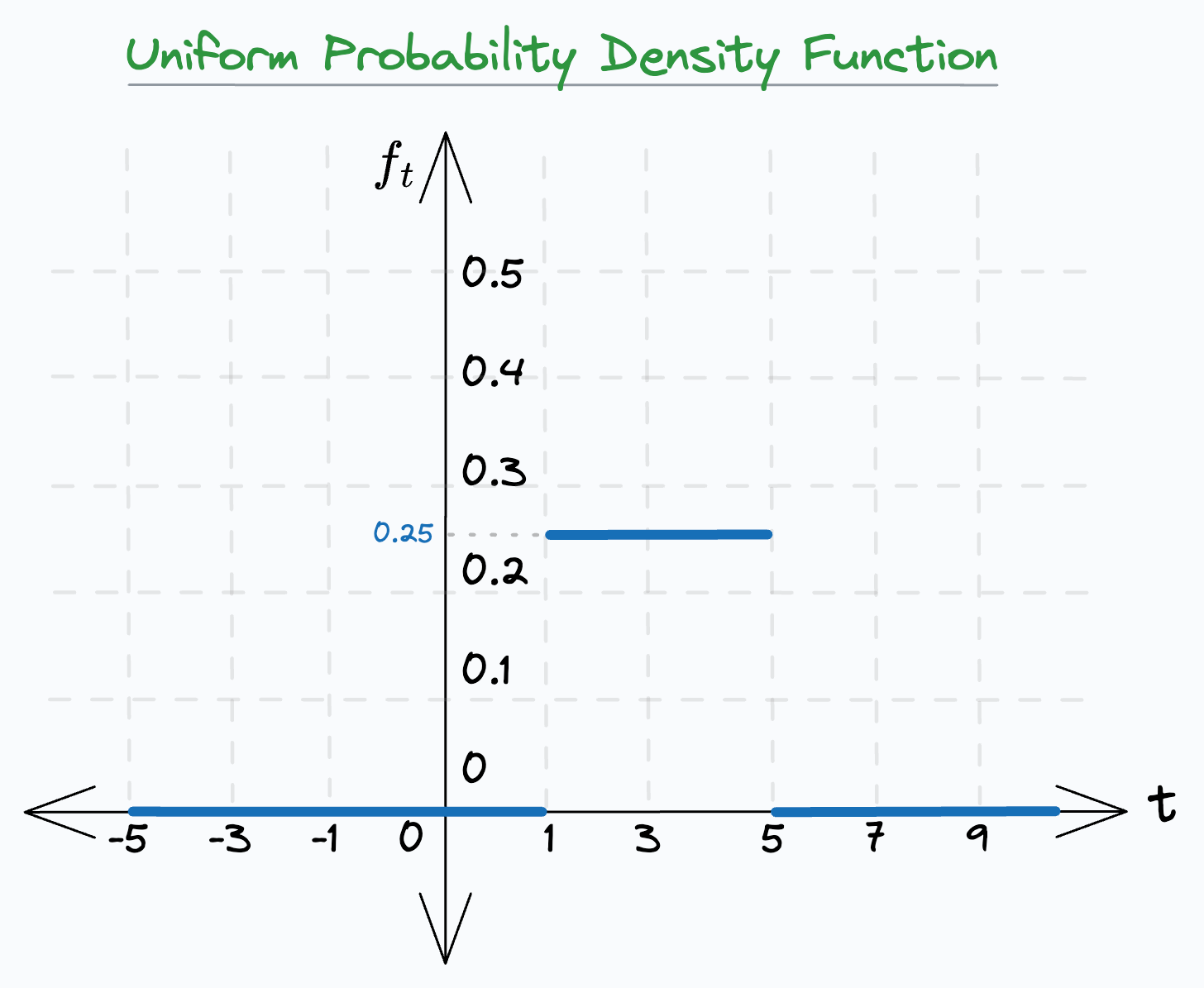
Consider the following probability density function of a continuous probability distribution. Say it represents the time one may take to travel from point A to B.

1. For simplicity, we are assuming a uniform distribution in the interval [1,5].

2. Essentially, it says that it will take somewhere between 1 and 5 minutes to go from A to B. Never more, never less.

Thus, the probability density function (PDF) can be written as follows:

\(f_{T}(t) = \left\{ \begin{array}{cl} \frac{1}{5-1} & : \ 1 \leq t \leq 5 \\ 0 & : \ \text{otherwise} \end{array} \right.\)

My question is: What is the probability that one will take precisely three minutes P(T=3)to reach point B?

• A) 1/4 (or 0.25)

• B) Area under the curve from t=[1,3].

• C) Area under the curve from t=[3,5].

• D) It cannot be determined.

Decide on an answer before you read further.

---

Well, all of the above answers are wrong.

The correct answer, however, is ZERO.

And I intentionally kept only wrong answers here so that you never forget something fundamentally important about continuous probability distributions.

Let’s dive in!

---

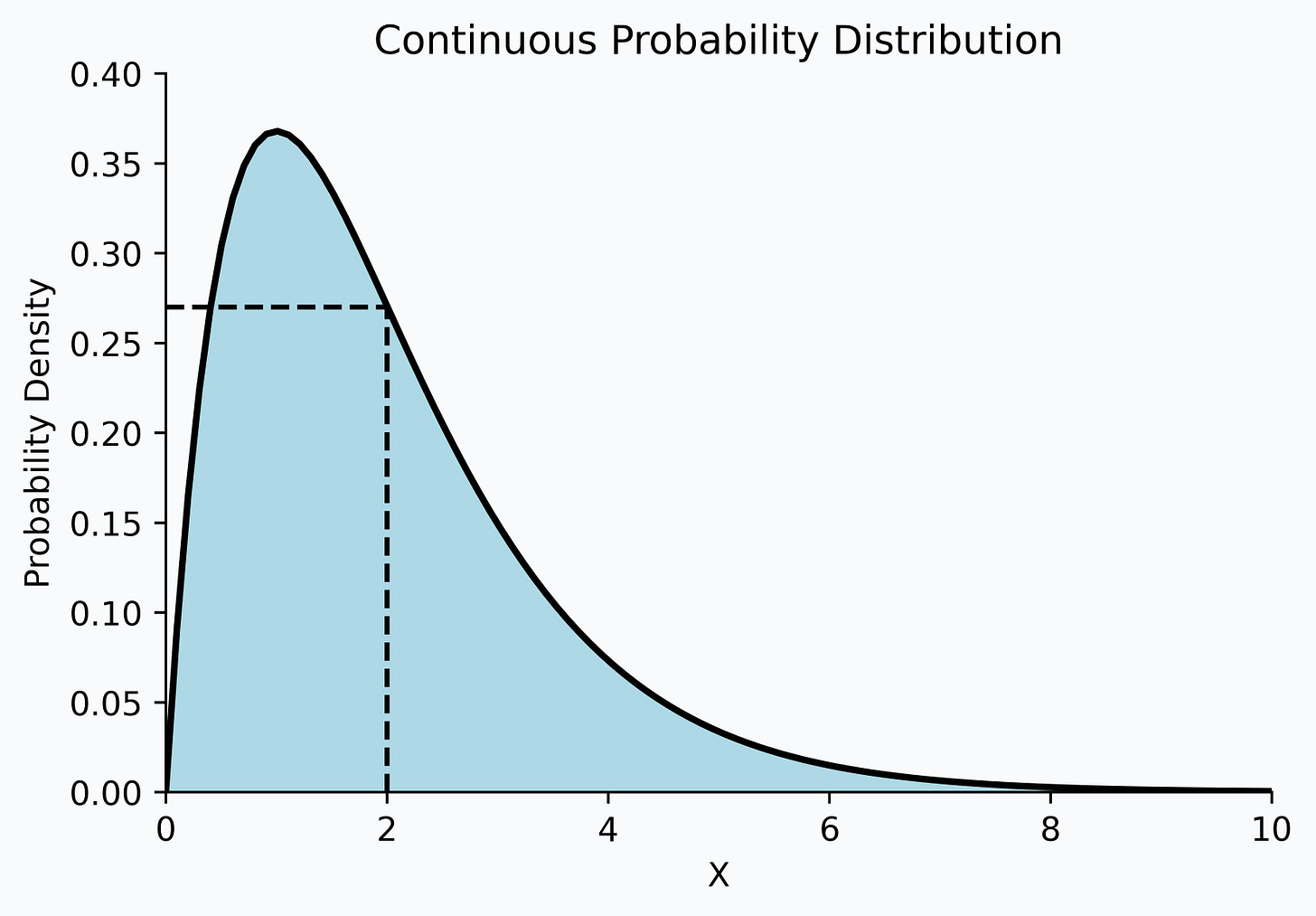
The probability density function of a continuous probability distribution may look as follows:

Some conditions for this probability density function are:

• It should be defined for all real numbers (can be zero for some values).

\(PDF \rightarrow f_{X}(x) \ ; \ x \in \mathbb{R}\)

This is in contrast to a discrete probability distribution which is only defined for a list of values.

• The area should be 1.

\(\int_{-\infty }^{\infty} f_{X}(x) \ dx = 1\)

• The function should be non-negative for all real values.

\(f_{X}(x) \geq 0 \ \ \forall \ \ x\)

Here, many folks often misinterpret that the probability density function represents the probability of obtaining a specific value.

For instance, by looking at the above probability density function, many incorrectly conclude that the probability of the random variable X being 2 is close to 0.27.

\(P(X=2) = 0.27\)

But contrary to this common belief, a probability density function:

• DOES NOT depict the probabilities of a specific value.

• is not meant to depict a discrete random variable.

Instead, a probability density function:

• depicts the rate at which probabilities accumulate around each point.

• is only meant to depict a continuous random variable.

Now, there are infinitely possible values that a continuous random variable may take.

So the probability of obtaining a specific value is always zero (or infinitesimally small).

Thus, answering our original question, the probability that one will take three minutes to reach point B is ZERO.

So what is the purpose of using a probability density function?

In statistics, a PDF is used to calculate the probability over an interval of values.

Thus, we can use it to answer questions such as…

• What is the probability that it will take between:

  • 3 to 4 minutes to reach point B from point A, or,

  • 2 to 4 minutes to reach point B from point A, and so on…

And we do this using integrals.

More formally, the probability that a random variable X will take values in the interval [a,b] is:

\(P(a \leq X \leq b) = \int_{a}^{b} f_{X}(x) \ dx\)

Simply put, it’s the area under the curve from [a,b].

From the above probability estimation over an interval, we can also verify that the probability of obtaining a specific value is indeed zero.

By substituting b=a, we get:

So remember…

In a continuous probability distribution:

• The probability density function does not depict the exact probability of obtaining a specific value.

• Estimating the probability for a precise value of the random value makes no sense because it is infinitesimally small.

• Instead, we use the probability density function to calculate the probability over an interval of values.

Any further follow-up questions? Feel free to reach out :)

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

---

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!

---

I like to explore, experiment and write about data science concepts and tools. You can read my articles on Medium. Also, you can connect with me on LinkedIn and Twitter.