Why Mean Squared Error (MSE)?
Why not any other loss function?
Say you wish to train a linear regression model. We know that we train it by minimizing the squared error:
But have you ever wondered why we specifically use the squared error?
See, many functions can potentially minimize the difference between observed and predicted values. But of all the possible choices, what is so special about the squared error?
In my experience, people often say:
Squared error is differentiable. That is why we use it as a loss function. WRONG.
It is better than using absolute error as squared error penalizes large errors more. WRONG.
Sadly, each of these explanations are incorrect.
But approaching it from a probabilistic perspective helps us truly understand why the squared error is the most ideal choice.
Let’s begin.
In linear regression, we predict our target variable y using the inputs X as follows:
Here, epsilon is an error term that captures the random noise for a specific data point (i).
We assume the noise is drawn from a Gaussian distribution with zero mean based on the central limit theorem:
Thus, the probability of observing the error term can be written as:
Substituting the error term from the linear regression equation, we get:
For a specific set of parameters θ, the above tells us the probability of observing a data point (i).
Next, we can define the likelihood function as follows:
The likelihood is a function of θ. It means that by varying θ, we can fit a distribution to the observed data and quantify the likelihood of observing it.
We further write it as a product for individual data points because we assume all observations are independent.
Thus, we get:
Since the log function is monotonic, we use the log-likelihood and maximize it. This is called maximum likelihood estimation (MLE).
Simplifying, we get:
To reiterate, the objective is to find the θ that maximizes the above expression.
But the first term is independent of θ. Thus, maximizing the above expression is equivalent to minimizing the second term.
And if you notice closely, it’s precisely the squared error.
Thus, you can maximize the log-likelihood by minimizing the squared error.
And this is the origin of least-squares in linear regression.
See, there’s clear proof and reasoning behind for using squared error as a loss function in linear regression.
Nothing comes from thin air in machine learning :)
But did you notice that in this derivation, we made a lot of assumptions?
Firstly, we assumed the noise was drawn from a Gaussian distribution. But why?
We assumed independence of observations. Why and what if it does not hold true?
Next, we assumed that each error term is drawn from a distribution with the same variance σ. But what if it looks like this:
In that case, the squared error will come out to be:
How to handle this?
This is precisely what I have discussed in today’s member-only blog.
In other words, have you ever wondered about the origin of linear regression assumptions? The assumptions just can’t appear from thin air, can they?
Thus today’s deep dive walks you through the origin of each of the assumptions of linear regression in a lot of detail.
It covers the following:
An overview of linear regression and why we use Mean Squared Error in linear regression.
What is the assumed data generation process of linear regression?
What are the critical assumptions of linear regression?
Why error term is assumed to follow a normal distribution?
Why are these assumptions essential?
How are these assumptions derived?
How to validate them?
What measures can we take if the assumptions are violated?
Best practices.
All in all, a literal deep-dive on linear regression. The more you will learn, the more you will appreciate the beauty of linear regression :)
👉 Interested folks can read it here: Where Did The Assumptions of Linear Regression Originate From?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
Thanks for reading!









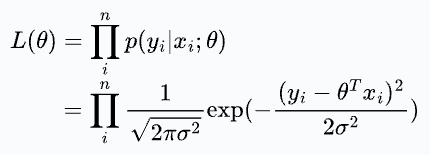
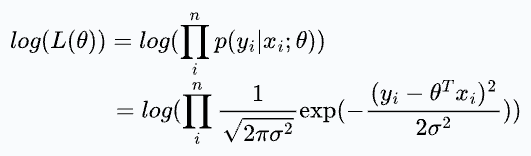





Good post Avi!